- Форми запису чисел.
Дійсні числа в пам’яті ЕОМ можуть представлятися у двох формах: з фіксованою та плаваючою комою.
При використанні формату з фіксованою комою окремо зберігаються ціла та дробова частини, як звичайні цілі числа. Таке представлення не має широкого застосування у зв’язку з малим діапазоном допустимих значень.
Значно кращим є формат з плаваючою комою або експоненціальний формат, який запропоновував у 1937р. німецький вчений Кондад Цузе. При використанні цього формату довільне дійсне число представляється у вигляді:
x = a·Qm,
де
a – мантиса,
m – порядок,
Q – основа системи числення, в якій записане число.Мантиса задає значущі цифри числа, а порядок вказує місцезнаходження крапки.
Наведемо приклади чисел, записаних у форматі з плаваючою комою.
Формат з фіксованою комою Формат з плаваючою комою 17510 0.175×103 18,7510 0.1875×102 10010,112 0.10010112 × 102111 У програмуванні використовують нормалізоване представлення числа, тобто числа, у якого мантиса задовольняє умовам
Отже, для збереження дійсного числа необхідно зберегти мантису і порядок. Оскільки обсяг пам’яті для збереження мантиси є скінченим, то можна говорити про кількість цифр числа, які можуть бути збережені. Їх ще називають значущими цифрами числа.
- Коди чисел, прямий, зворотний та модифікований.
Коди чисел
Будь-яка інформація (числа, команди, записи і т. п.) представляється в ЕОМ у вигляді двійкових кодів фіксованої або змінної довжини.
Окремі елементи двійкового коду, що мають значення 0 або 1, називають розрядами або бітами.
Вісім бітів — байт.
У ЕОМ з метою спрощення виконання арифметичних операцій застосовують спеціальні коди для подання чисел. Використання кодів дозволяє звести операцію віднімання чисел до арифметичного додавання кодів цих чисел.
Застосовуються прямий, зворотний і додатковий коди чисел.
Прямий код використовується для представлення негативних чисел в запам’ятовуючому пристрої ЕОМ, а також при множенні і діленні.
Зворотний і додатковий коди використовуються для заміни операції віднімання операцією додавання, що спрощує будову арифметичного блоку ЕОМ. До кодів висуваються наступні вимоги:
- Розряди числа в коді жорстко зв’язані з певною розрядною сіткою.
- Для запису коду знаку в розрядній сітці відводиться фіксований, строго визначений розряд.
Наприклад, якщо за основу представлення коду взято один байт, то для представлення числа буде відведено 7 бітів, а для запису коду знаку один розряд.
Прямий код. Прямий код двійкового числа співпадає по зображенню із записом самого числа. Значення знакового розряду для позитивних чисел дорівнює 0, а для від’ємних чисел 1.
Знаковим розрядом зазвичй є крайній розряд в розрядній сітці. Надалі при запису коду знаковий розряд від цифрових, домовимося відокремлювати комою. Якщо кількість розрядів коду не зазначено, будемо припускати, що під запис коду виділено один байт.
Приклад. У випадку, коли для запису коду виділений один байт:- для числа +1101
- 0,0001101 — прямий код
- для числа -1101
- 1,0001101 — прямий код
Зворотний код. Зворотний код для невід’ємного числа збігається з прямим кодом.
Для від’ємного числа всі цифри числа замінюються на протилежні (1 на 0, 0 на 1), а в знаковий розряд заноситься одиниця.Приклад.- Для числа +1101
- 0,0001101 — прямий код
- 0,0001101 — зворотний код
- Для числа -1101
- 1,0001101 — прямий код
- 1,1110010 — зворотний код
Додатковий код. Додатковий код невід’ємного числа збігається з прямим кодом.
Для від’ємного числа додатковий код утворюється шляхом отримання зворотного коду і додаванням до молодшого розряду одиниці.Приклад.- Для числа +1101
- 0,0001101 — прямий код
- 0,0001101 — зворотний код
- 0,0001101 — додатковий код
- Для числа -1101
- 1,0001101 — прямий код
- 1,1110010 — зворотний код
- 1,1110011 — додатковий код
Особливості складання чисел у зворотному та додатковому кодах
При додаванні чисел в додатковому коді, одиниця переносу, що виникла, в знаковому розряді відкидається.
При додаванні чисел у зворотному коді одиниця переносу, що виникла, в знаковому розряді додається до молодшого розряду суми кодів.
Якщо результат арифметичних дій є кодом від’ємного числа, необхідно перетворити його в прямий код. При цьому зворотний код перетворюється в прямий заміною цифр у всіх розрядах, крім знакового на протилежні. Додатковий код перетворюється в прямий також, як і зворотний, з подальшим додаванням одиниці до молодшого розряду.
Приклад
Скласти двійкові числа X й Y в зворотному та додатковому кодах.
а) X= 111, Y= -11;
1) Складемо числа, користуючись правилами двійкової арифметики:
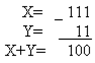
2) Складемо числа, використовуючи коди:
Прямий код Складання в зворотному коді Складання в додатковому коді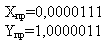 
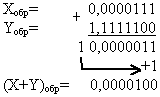
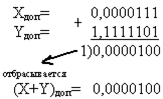
Так як результат додавання являється кодом додатного числа (знак 0), то (X+Y)звор=(X+Y)дод=(X+Y)пр.
б) X= -101,Y= -11;
1) Складемо числа, користуючись правилами двійкової арифметики:
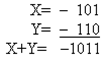
2) Складемо числа, використовуючи коди:
Прямий код Додавання в зворотньому коді Додавання в додатковому коді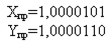 
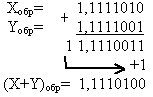
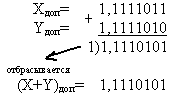
Оскільки сума є кодом від’ємного числа (знак 1), то необхідно перевести результати в прямий код: – з зворотного коду (X+Y)звор=1,1110100
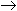(X+Y)пр=1,0001011; – з додаткового коду (X+Y)дод=1,1110101 
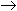(X+Y)пр=1,0001010+0,0000001=1,0001011. Таким чином, X+Y= -1011 й отриманий результат співпадає з звичайним записом.Модифіковані зворотний й додатковий коди
При переповненні розрядної сітки, відбувається перенесення одиниці в знаковий розряд. Це призводить до неправильного результату, при чому додатне число, що вийшло в результаті арифметичної операції може сприйматися як від’ємне (тому що у знаковому розряді “1”) і навпаки.
Наприклад:
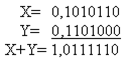
Тут X і Y – коди додатних чисел, але ЕОМ сприймає результат їх складання як код від’ємного числа (“1” в знаковому розряді). Для виявлення переповнення розрядної сітки вводяться модифіковані коди.
У модифікованому зворотному і модифікованому додатковому кодах під знак числа відводиться не один, а два розряди: “00” відповідає знаку “+”, “11” – знаку “-“. Будь-яка інша комбінація (“01” або “10”), що вийшла в знакових розрядах слугує ознакою переповнення розрядної сітки. Додавання чисел в модифікованих кодах нічим не відрізняється від складання в звичайних зворотному і додатковому кодах.
Розглянемо попередній приклад, виконавши додавання в модифікованому зворотному коді:
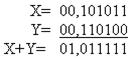
Комбінація “01” в знакових розрядах значить, що відбулося переповнення і отриманий результат – невірний.
Розглянемо ще один приклад. Приклад. Дані два числа: X=101001 й Y= -11010. Скласти їх в модифікованому додатковому коді.
1) Переведемо X та Y в модифікований додатковий код:
Звичайний запис Модифікований зворотний код Модифікований додатковийкод X= +101001Y= -011010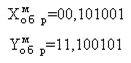 
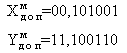
2) Виконаємо складання:
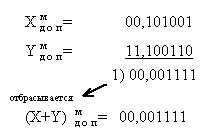
Переповнення немає (в знакових розрядах “00”), тому отриманий результат – вірний (X+Y=1111)
- Подання текстових, графічних і звукових даних у комп'ютері.
Представлення символьної інформації
При збереженні довільного тексту в пам’яті ЕОМ, його розглядають як послідовність символів. Кожному символу ставиться у відповідність деякий фіксований двійковий код, довжина якого може бути різною (8 біт, 7 біт, 16 біт і ін.). Оскільки такий код однозначно визначає ціле число, то можна скати, що кожному символу ставиться у відповідність деяке ціле число.
Відповідність між символами і кодами символів встановлюється за допомогою кодових таблиць. З розвитком інформаційних технологій було розроблено багато таких таблиць, які відрізняються кількістю біт та кодами, які ставляться у відповідність символам. Тому при передачі текстової інформації вимагається, щоб у одержувача текстової інформації при декодуванні використовувалась та ж сама кодова таблиця, яку використовував відправник при її кодуванні. В іншому випадку, декодування призводить до спотворення інформації. У зв’язку з цим, Інститут стандартизації США (ANSI – American National Standard Institute) ввів у дію систему кодування ASCII (American Standart Code for Information Interchange – американський стандартний код для обміну інформацією). В цій системі кожному символу ставиться у відповідність двійковий код довжиною 8 біт=1 байт, тобто кількість різних символів, яка може бути закодована рівна 28 = 256
Система кодування ASCII містить дві таблиці – базову та розширену.
Базова таблиця встановлює відповідність між символами та кодами від 0 до 127, а розширена – від 128 до 255.
Коди від 0 до 31 базової таблиці відведено для керуючих кодів, які використовуються для керування виводом текстової інформації. Починаючи з коду 32 розміщено символи англійського алфавіту, розділові знаки, цифри та ін.
Представлення графічної інформації
Графічна інформація може подаватися за допомогою графічних зображень: малюнків, креслень, фотографій, зображень на екрані монітора, телевізора і т.д. По своїй структурі графічні зображення можуть бути растровими та векторними.
Растрове зображення складається з маленьких точок – пікселів (PIХEL–PICture’S Element – елемент зображення). Піксель є мінімальним елементом зображення одного кольору.
Весь масив пікселів називають растром (від латинського “rastrum”–граблі).
Кількість пікселів, які припадають на одиницю довжини, характеризують роздільну здатність растру. Значення роздільної здатності записують в одиницях dpi (doter per inch – кількість точок на одному дюймі (2,54см).
Масив пікселів розбито на рядки і стовпці. Таким чином, кожен піксель має координати (х,у), де х – номер рядка, у – номер стовпця, на перетині яких він знаходиться. Отже, для збереження растрового графічного зображення необхідно зберегти інформацію про колір кожного пікселя. При цьому кожному кольору ставиться у відповідність деяке число. Кількість біт, яку виділяють для збереження кольору одного пікселя, називають глибиною кольору. Глибина кольору визначає скільки різних кольорів може бути збережено. Так кількість різних кольорів при глибині кольору n бітів дорівнює 2n, як кількість різних комбінацій з n символів двійкового алфавіту.
Приклад. Розглянемо вміст растрового графічного файлу при збереженні монохромного зображення. Таке зображення характерне тим, що для збереження кольору одного пікселя необхідно всього один біт (наприклад, 0 – білий колір, 1 – чорний).
Приклад монохромного зображення
При збереженні кольорового зображення, для представлення кольору використовується адитивна кольорова модель RGB. Ця модель використовується для опису кольорів, які можуть бути отримані за допомогою пристроїв, що ґрунтуються на принципі випромінювання (наприклад, монітори) та змішування фарб (принтери). В якості основних кольорів вибрано червоний (Red), зелений (Green) та синій (Blue). Інші кольори та відтінки можуть бути отримані змішуванням певної кількості кожного з основних кольорів.
Історія системи RGB почалася з дослідів Томаса Юнга. Взявши три ліхтарі з світловими фільтрами червоного, зеленого і синього кольору, на білому екрані він одержав таке зображення Колір, який утворюється змішуванням трьох основних компонентів, можна представити вектором у тривимірній системі координат R, G і В, де координати виражають інтенсивності кожного з кольорів.
Чорному кольору відповідає центр координат – точка (0, 0, 0), білий колір виражено максимальним значенням компонентів. Нехай максимальне значення уздовж кожної осі дорівнює 1, тоді білий колір – це вектор (1, 1, 1).
Точки, що лежать на діагоналі куба від чорного до білого, мають однакові значення інтенсивності кожного з кольорів. Це градації сірого – їх можна вважати білим кольором різної яскравості. Загалом кажучи, якщо колір, тобто всі компоненти відповідного вектора (r, g, b), помножити на однаковий коефіцієнт k , то колір (kr, kg, kb) зберігається, змінюється тільки яскравість.
Дослідження показали, що не всі насичені кольори можуть бути представлені сумішшю зазначених трьох компонентів. Але не дивлячись на це, система RGB широко використовується на даний час в кольорових телевізорах і дисплеях комп'ютерів. Отже, при збереженні кольоровогозображення, потрібно зберегти колір кожного окремого пікселя, як інтенсивності складових кольорів.
Растрові зображення мають значний недолік, пов’язаний із якістю зображення. Як показано на рисунку растрового зображення, при його збільшенні зображення спотворюється. Звичайно, покращити якість зображення можна збільшивши кількість пікселів, але це призведе до збільшення об’єму пам’яті під час його збереження. Цього недоліку позбавлені векторні зображення, у яких розмір будь-якого елемента може бути змінений аж “до нескінченності”. Але таке зображення неможливо отримати шляхом сканування, оскільки кожний її елемент будується за допомогою геометричних об’єктів або примітивів, в якості яких можуть виступати лінії, дуги, кола і т.д. Саме завдяки тому, що зображення зберігається у вигляді набору математичних формул, які описують його елементи, векторна графіка дозволяє легко змінювати розміри статичних зображень без втрати чіткості їхніх меж.Векторна графіка створюється за допомогою спеціальних програмних засобів типу Adobe Photoshop, CorelDRAW та ін. Файли, в яких зберігають графічні зображення, називають графічними файлами. В залежності від типу графічного зображення, кількості присутніх у ньому кольорів, способу збереження (із стисненням, чи без) і т.д., розрізняють різні формати графічних файлів: BMP, JPEG, PNG, TIF, GIF, CDR, PSD і інші.
Представлення звукової інформації
З фізичної точки зору звук є неперервними коливаннями (неперервною звуковою хвилею), що можуть поширюватися в повітрі чи іншому пружному середовищі. Одиницею виміру звуку є децибели.
Звукова хвиля є неперервною (аналоговою), тому для її збереження застосовують розглянутий раніше метод дискретизації у часі. Кількість вимірів рівня звуку за одну секунду називають частотою дискретизації, і вимірюють у герцах (поширеними є частоти 22КГц та 44,1КГц). Зрозуміло, що чим більша частота дискретизації, тим більша якість збереженого звуку, але і більший об’єм пам’яті необхідний для його збереження. Якість звуку залежить також від розрядності перетворення – кількості біт, які виділяються для збереження одного виміру (поширеними величинами є 8, 16 та 24 біти).